| [Basic Algorithm] | [Extensions] | [Experimental Results] |
| [Appendix] User Guide | [Reference] | |
| Download: Test Data, Executable File, Source Code | ||
 |  |  |
| (a) Original image | (b) image by seam carving | (c) image by scaling |
Fig. 1 Comparison of seam carving and conventional image resizing (scaling). The signs are distorted in the scaled image, while keep the original shape in the image given by seam carving.
In this project, I implemented Seam Carving [1], a technique proposed by Shai Avidan and Ariel Shamir to resize images without distorting the primary content of the images. This technique works by removing the seams (i.e. least noticeable pixel-wide paths across or up-and-down an image), until the image is of the desired smaller size.
1. Basic Algorithm
The overall process of constructing photometric stereos basically consists of four steps:1.1 Optimal seam: Formally, let I be an n×m image and define a vertical seam to be:
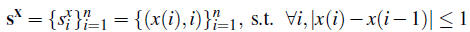 (1)
(1)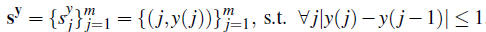 (2)
(2)Given an energy function e, we can define the cost of a seam as
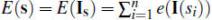 . The optimal seam is the one with minimum cost.
. The optimal seam is the one with minimum cost.The problem of looking for an optimal seam can be formulated as dynamic programming [1] or graph cut [2]. The dynamic programming approach consists of two steps: first, traverse the image from the first row to the last row and compute the cumulative minimum energy M (the energy of removing a partial seam for the top to the pixel (i, j)) for each entry (i, j):
 (3)
(3)1.2 Energy function: I use a simple energy function
 (4)
(4)1.3 Optimal Seams-Order: Image retargeting (i.e. an image I of size n×m is retargeted to size n0×m0) requires removing several horizontal and vertical seams. The order of romoving seams can be: vertical seams first, horizontal seams first, or alternate between the two. However, the optimal order can be found also using dynamic programming. The problem definition is
 (5)
(5)where k = r + c, r = (m - m'), c = (n - n') and  (αi denotes whether we remove a horizontal or vertical seam in step i).
(αi denotes whether we remove a horizontal or vertical seam in step i).
The transport map T is
 (6)
(6)
 (αi denotes whether we remove a horizontal or vertical seam in step i).
(αi denotes whether we remove a horizontal or vertical seam in step i).The transport map T is
 (6)
(6)where T(r, c) is the minimum cost of removing r horizontal and c vertical seam
| [Back to Top] | [Go to Next] |
-----------------------------------------------------------------------------------------------------
Copyright (c) 2009 Wei Zhang